身体運動学の基礎
身体運動学とは・・・?
骨や関節、筋などの運動器によって行われる身体運動に関する学問
運動学とは・・・?
運動を時空間で記述する学問のこと
ブリタニカ国際大百科事典より
また、運動学は以下の2つに分類される。
- 骨運動学:対象が骨体の運動(骨運動)
- 関節運動学:対象が関節面に生じる運動(関節包内運動)
基本肢位
- 基本肢位
-
身体動作を比較したり評価する際に、基準となる姿勢
- 解剖学的立位肢位
-
体幹正中位で顔面が正面を向き、上肢は掌を前方に向け下垂、下肢は平行にして足趾を前方に向けた姿勢
- 基本的立位肢位
-
解剖学的立位肢位は掌が正面を向いているが、基本的立位肢位は対側に向いている姿勢
- 体位
-
身体が重力の方向とどのような関係にあるかを示す
| 名称 | 読み方 | 詳細 |
|---|---|---|
| 背臥位・仰臥位 | はいがい・ぎょうがい | 背側を下にして寝ている状態 |
| 腹臥位 | ふくがい | 腹側を下にして寝ている状態 |
| 側臥位 | そくがい | 横向きになって寝ている状態 |
| 座位 | ざい | 体幹を起こし臀部で体重を支持している状態 |
| 長座位 | ちょうざい | 足をまっすぐに伸ばし床面に座った状態 |
| 立位 | りつい | 足底で支持して立った状態 |
運動と変位
- 位置
-
空間内における物体のある場所
- 運動
-
物体の位置の時間的変化
- 並進運動:物体状のすべての点が平行に同じ距離を移動する運動
- 回転運動:物体状のすべての点が空間に固定された回転中心の周りを回転する運動
※人体の多くの関節は回転運動と並進運動が複合して運動を行なっている
- 変位
-
物体が運動を行い、動き始めた場所から動き終えた場所までの移動した量(変化量)
- 速度・加速度
-
速度:物体の移動した軌跡が直線である運動を行った場合の単位時間あたりの変位
加速度:単位時間あたりの速度の変化量
- 角速度・角加速度
-
角速度:物体が回転運動を行った場合の単位時間あたりの角度の変化量
角加速度:単位時間あたりの角速度の変化量
運動の面と軸
- 前額面
-
床面に対して垂直で前後に二分する面。この面に直行する前後方向の軸を矢状軸という
- 矢状面
-
床面に対して垂直で左右に二分する面。この面に直行する左右方向の軸を前額軸という
- 水平面
-
床面に対して平行で上下に二分する面。この面に直行する上下方向の軸を水平軸という
運動連鎖
運動力学
力の概念
- 『力』とは
-
運動を引き起こしたり変化させたりする能力の量。単位はニュートン(N)
1N=質量1kgの物体に、1m/s2の加速度を生じさせる力のこと
(重力加速度は約9.8m/s2で、N=質量(kg)×9.8(m/s2)
- 『質量』とは
-
物体を構成する『物質の量』を表す。単位はKgである
- 『重量』とは
-
物体に作用する重力であり質量と重力加速度の積を表す。
よって質量1kgの物体の重量は1×9.8=9.8Nとなる
- 『ベクトル』とは
-
ベクトルとは力や速度などの大きさに向きを付加した量である
力と運動
- 『慣性』と『慣性の法則』
-
・『慣性』とは物体が運動状態を変えることに抵抗する性質
- 『運動の法則』とは
-
物体に力が生じると『加速度』が生じる
この加速度が物体の受ける力に比例し、物体の質量に反比例すること
(運動方程式 F=ma F=力 m=質量 a=加速度)
- 『作用反作用の法則』とは
-
あらゆる力に対して、同じ大きさで反対向きの力が必ず働くこと
- 『応力』とは
-
運動に伴い、体に様々な力が作用する。その時に物体に加えられた単位面積あたりの力のこと
応力は身体内部で産生される『内力』・重力や外からの負荷による『外力』によって生じる
仕事とエネルギー
- 仕事とは
-
物体に力を加えて変化させること(仕事=力(N)×変位した距離(m))
単位はジュール(J)で表される(1Nの力で1mだけ物体を移動させた時の仕事は1Jである)
単位時間あたりの仕事をする能力は仕事率(パワー)という。単位はワット(W)
- エネルギーとは
-
物体が持つ仕事をする能力。仕事の総量とエネルギーの総量は等しい。単位はジュール(J)
- 力学的エネルギーとは
-
力学的な量によって決定されるエネルギー。運動エネルギーと位置エネルギーからなる。
- 運動エネルギー:運動してる物体が持つエネルギー(速くなるほど大きくなる)
- 位置エネルギー:物体がその位置にあるために発生するエネルギー(高い位置にあるほど大きい)
- 保存力・非保存力とは
-
- 保存力:重力や弾性力などの力により位置エネルギーの定義が明白にできる力
- 非保存力:保存力以外の力(摩擦や空気抵抗など)
非保存力が物体に作用しない場合、保存力のみを受けて運動する場合は運動エネルギーと位置エネルギーの和は一定に保たれる。(力学的エネルギー保存の法則=振り子運動などがあたる)
身体運動とモーメント
力のモーメント
- 力のモーメントとは
-
ある回転軸の回に剛体を回転させる作用の大きさのこと(トルクとしても表される)
(剛体とは:外力が加わっても形や大きさの変わらない力学上の仮想的な物体)
力のモーメントは力の大きさ(N)とモーメントアーム(m)の積で算出される(N・m)
- モーメントアーム
-
回転軸から力の作用線までの直線距離(レバーアームともいう)
- 慣性モーメント
-
回転運動の角速度変化に対して抵抗性を示す量
質量が同じであっても回転軸からの距離が長いほど慣性モーメントは大きくなる
重心
- 重心とは
-
物体の各部に働く重力を1つにまとめ、それが作用する点である
※質量中心とよく混同されるが定義は違う。質量中心は「物体の質量を正確な中心とみなせる点」である
しかし、重力化においては質量中心ではなく重心として呼ばれるため混同しがちである。
- 重心線と床反力
-
重心線とは:重心から地球の中心に向かう仮想の線
床半力とは:物体が床面と接触している部分から生じる反力
- 支持基底面
-
隣接する接触面の外周によって作られる領域のことである
支持基底面が広いほど安定性は高まる。重心線が支持基底面の中心に近いほど安定性が高まる
身体運動とてこ
てこは、
- 支点:てこの支え回転の中心になる場所
- 力点:てこに力を加える場所
- 作用点:加えた力が働き場所
からなり、3つの種類がある。
第1のてこ
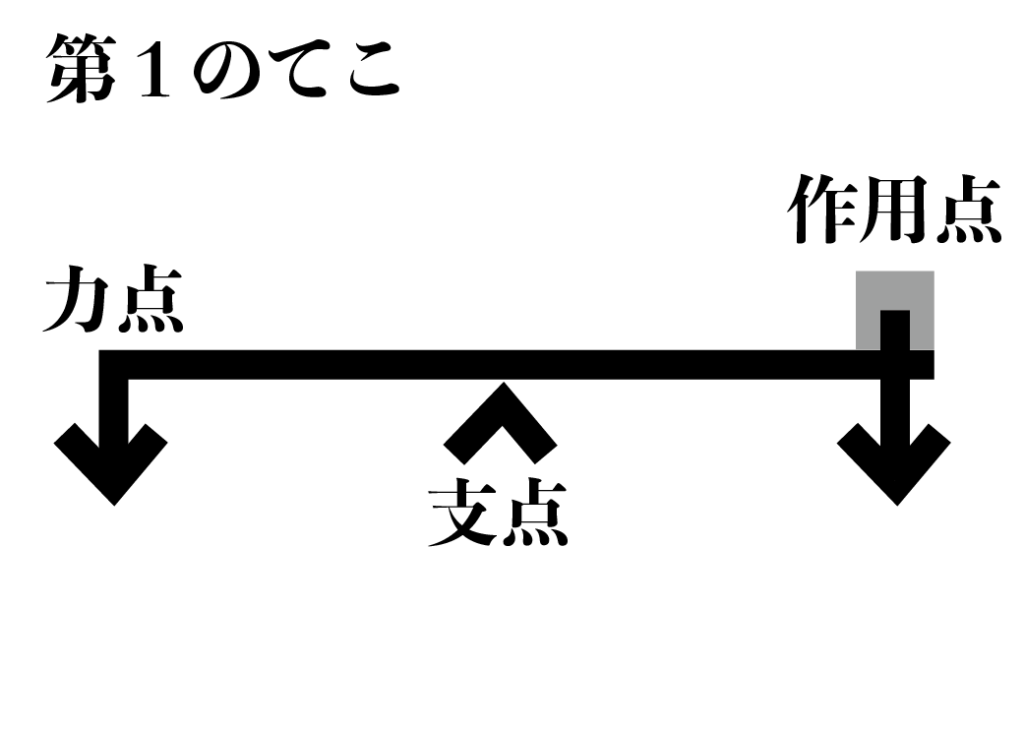
- 支点が力点と作用点の間
- バランスのてこと呼ばれる
- 特徴は安定性
- 股関節など
第2のてこ
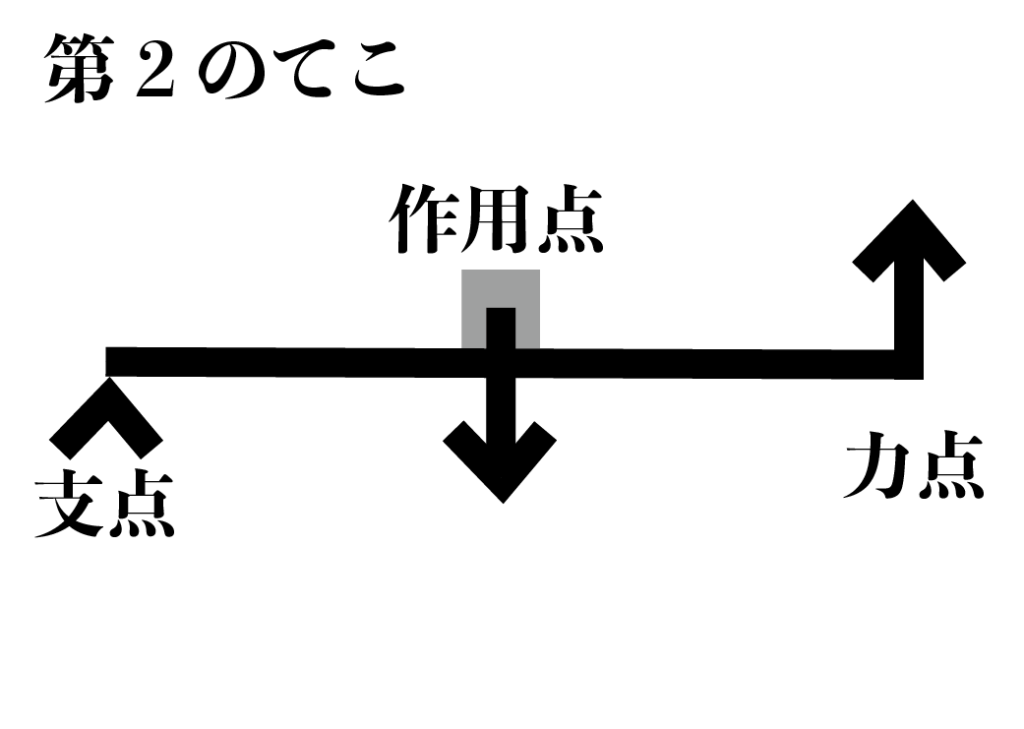
- 作用点が支点と力点の間
- 力に有利なてこ
- 顎関節など
第3のてこ

- 力点が支点と作用点の間
- 力には不利
- 速さには有利
- 肩関節など
関節モーメントと関節応力
- 外部モーメント
-
身体外部から加わる外力によって産生されるモーメント
- 内部モーメント
-
身体内部で生じる内力によって産生されるモーメント
- 関節モーメント
-
内部モーメントの中で、関節を回転させる力のモーメント
- 関節応力とは
-
関節に作用する外力・内力により関節面には負荷がかかる。この応力に対して関節面に生じる抵抗力
てこの支点に作用する応力がこの力に相当する
関節に作用するモーメント
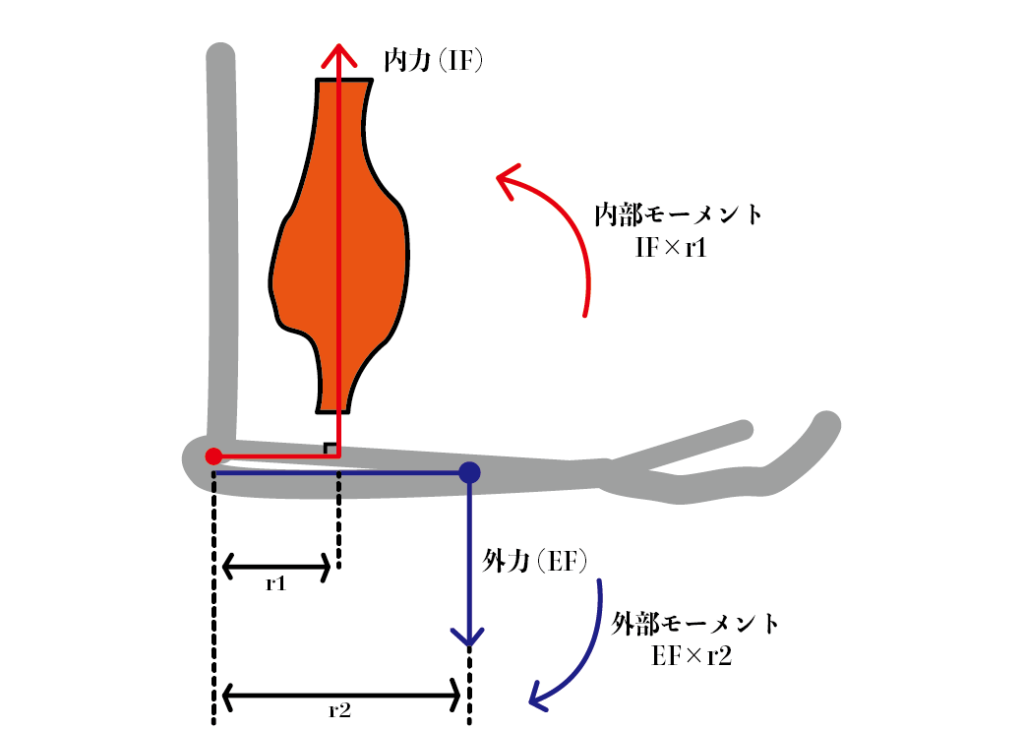
モーメントの変化①

モーメントの変化②
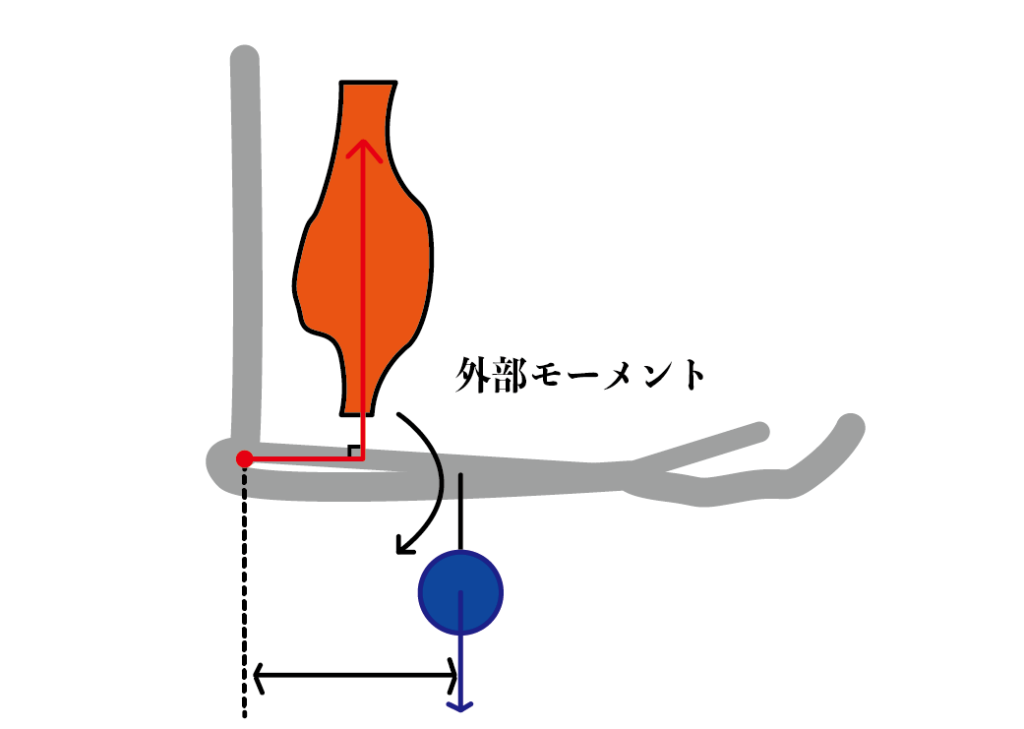
①と②を比較した際、①のように重りが肘関節から遠位部にあればあるほどモーメントアームは長くなり
それに伴って、肘関節の外部モーメントの値も大きくなる。ゆえに発揮しなければならない筋力も増える。
逆に②では重りが肘関節に対してより近位にあるのでモーメントアームは短くなり、肘関節の外部モーメントも
減少する。故に発揮する筋力も少なくて済む。

